3. Graphs and advanced graphs
Table of Contents
A. General Introduction
A graph is a collection of nodes and edges. Each node is connected to other nodes by edges. The connection between nodes can either be directed or undirected. Furthermore, each edge can even have a weight.
A graph can be represented in a number of ways. I have listed two common representations:
- Adjacency List
- All the nodes are stores in a hashmap. The key is the node and the value is an array of all the nodes that are connected to the key node.
- Adjacency Matrix
- A 2D array that stores the connections between nodes. The value at index
(i,j)is 1 if there is an edge between nodeiand nodej. - In case of undirected graphs, the value at index
(i,j)and(j,i)need not be symmetrical.
- A 2D array that stores the connections between nodes. The value at index
Key Ideas:
-
The number of incoming and outgoing edges of a node is called indegree and outdegree, respectively.
-
The degree of a node is the number of incoming and outgoing edges.
-
A directed graph is acyclical if there are no cycles in the graph. That is, all the directed edges in the graph does not form a closed loop.
I. Adjacency List
Time complexities
| Operation | Worst-case Time complexity |
|---|---|
| Add node (N) | O(1) |
| Add edge (E) | O(1) |
| Remove node (N) | O(N+E) |
| Get adjacent nodes | O(1) |
| Check if node is adjacent | O(n) |
Space complexity: O(N+E)
II. Adjacency Matrix
Time complexities
| Operation | Worst-case Time complexity |
|---|---|
| Add node (N) | O(N^2) |
| Add edge (E) | O(1) |
| Remove node (N) | O(1) |
| Get adjacent nodes | O(N) |
| Check if node is adjacent | O(1) |
Space complexity: O(N^2)
B. Leetcode problems
133. Clone Graph
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node:
val:int
neighbors: List[Node]
Test case format:
For simplicity, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example:

Key Ideas
- Maintain a hashmap to track the clone of each node
- use a graph traversal algorithm to clone the graph
- Pop a node from the queue/stack; check if the node has a clone in the hashmap; if not, create a clone and add it to the hashmap
- Iterate through neighbors and check if they have a copy and add it to the clone’s neighbors
- Maintain a visited set to avoid infinite loop
- Return the clone of the given node
Code
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
# 1. Have a hash map which tracks a new node for every old node
# 2. pop a node from the stack, check if there is a copy in map else, create a new one
# 3. start looping through neighbors and check if they have copy and add it to new node children
if node is None:
return None
old2new = {}
queue = [node]
visited = set()
while queue:
cur_node = queue.pop()
visited.add(cur_node)
if (cur_node in old2new) is False:
old2new[cur_node] = Node(cur_node.val)
new_node = old2new[cur_node]
for n in cur_node.neighbors:
if (n in old2new) is False:
old2new[n] = Node(n.val)
new_n = old2new[n]
new_node.neighbors.append(new_n)
if n not in visited:
queue.append(n)
visited.add(n)
return old2new[node]
994. Rotting Oranges
You are given an m x n grid where each cell can have one of three values:
- 0 representing an empty cell,
- 1 representing a fresh orange, or
- 2 representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example:

Key Ideas
-
An easy way to iterate level by level is to use an inner loop to iterate
knumber of times, wherekis length of the queue at the start of inner loop.while queue: q_len = len(queue) for _ in range(q_len): ... # do somethingThis formulation can be used for multi-source BFS.
-
Use a counter variable to track the number of fresh oranges
Code
from collections import deque
from itertools import product
class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
time_step = 0
fresh_oranges = 0
m,n = len(grid), len(grid[0])
DIRECTIONS = [(1,0), (0,1), (-1, 0), (0, -1)]
check_valid_coord = lambda x, y: x >=0 and x < m and y >= 0 and y < n
queue = deque([])
for i,j in product(range(m), range(n)):
if grid[i][j] == 2:
queue.append((i,j))
if grid[i][j] == 1:
fresh_oranges += 1
while queue and fresh_oranges > 0:
time_step += 1
q_len = len(queue)
for _ in range(q_len):
x,y = queue.popleft()
for dx, dy in DIRECTIONS:
xx,yy = x+dx, y+dy
if check_valid_coord(xx,yy) and grid[xx][yy] == 1:
grid[xx][yy] = 2
queue.append((xx,yy))
fresh_oranges -= 1
if fresh_oranges > 0:
return -1
return time_step
Time complexity: O(m*n), where m is the number of rows and n is the number of columns.
Space complexity: O(m*n), in worst case, the queue is filled with all the coordinates in the grid.
684. Redundant Connection
In this problem, a tree is an undirected graph that is connected and has no cycles.
You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.
Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.
Example 1:
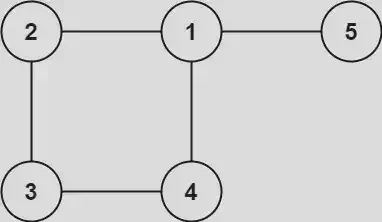
Answer: [1,4]
Key Ideas
- Represent the graph as an adjacency list
- Maintain a results list, which contains the edges that can be removed.
- Iterate through the edges
- If two nodes are already connected, add the edge to results list
- else: connect the nodes with the edge
- return the last element in the results list
Code
from collections import defaultdict, deque
class Graph:
def __init__(self, N:int) -> None:
self.N = N
self.edges = defaultdict(list)
def connect(self, p:int, q:int) -> None:
self.edges[p].append(q)
self.edges[q].append(p)
def is_connected(self, p:int, q:int) -> bool:
if p in self.edges[q]:
return True
queue = deque([p])
visited = set()
while queue:
node = queue.popleft()
visited.add(node)
if node == q:
return True
for child in self.edges[node]:
if child not in visited:
queue.append(child)
visited.add(child)
return False
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
g = Graph(n)
result = []
for edge in edges:
p = edge[0]
q = edge[1]
connected = g.is_connected(p,q)
if connected is False:
g.connect(p,q)
continue
result.append(edge)
return result[-1]
Time complexity: O(n^2),
Space complexity: O(n^2).
743. Network Delay Time
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.
We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.
Example:
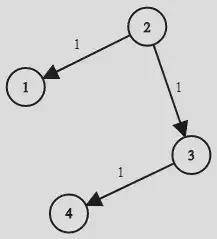
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2
Key Ideas
- Use a
min-heapto store the nodes and their corresponding time - When iterating through the edges, add the time to the current time and push it to the heap
- Use a min_time variable to track the minimum time taken to reach all the node
- Finally, check if the all the nodes were visited
- If not, return -1
- Else, return the min_time
Code
import heapq
from collections import defaultdict
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
graph = defaultdict(list)
for u,v,w in times:
graph[u].append((v,w))
queue = [(0, k)] # time, node
visited = set()
min_time = 0
while queue:
time, node = heapq.heappop(queue)
if node in visited:
continue
visited.add(node)
min_time = max(min_time, time)
for child_node, child_time in graph[node]:
if child_node not in visited:
heapq.heappush(queue, (time+child_time, child_node))
return min_time if len(visited) == n else -1
1584. Min Cost to Connect All Points
You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
Example:
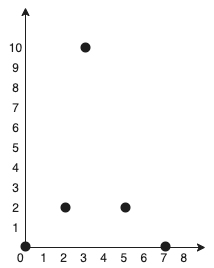
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
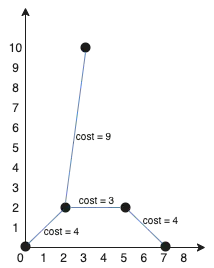
We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points.
Key Ideas:
- Goal: Path which connects all the points at the minimum cost
- Use a min-heap to store the cost for each node combination that can be explored
- Use a set to track the visited nodes
- Iterate till the visited set is equal to the number of nodes
- At every pop, check if the node is already visited
- If yes, skip the node and continue
- Else, add the node to the visited set
- Add the cost of the node to the path_cost variable
- explore the children
Code
from collections import defaultdict
import heapq
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
mhat_dist = lambda x1, y1, x2, y2: abs(x1 - x2) + abs(y1 - y2)
graph = defaultdict(list)
for i, (x1,y1) in enumerate(points):
for j in range(i+1, len(points)):
x2, y2 = points[j]
dist = mhat_dist(x1,y1, x2, y2)
graph[i].append((dist, j))
graph[j].append((dist, i))
queue = [(0,0)]
visited = set()
min_cost = 0
while len(visited) < len(points):
cost, pt = heapq.heappop(queue)
if pt in visited:
continue
visited.add(pt)
min_cost += cost
for w, cpt in graph[pt]:
if cpt not in visited:
heapq.heappush(queue, (w, cpt))
return min_cost
778. Swim in Rising Water
You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).
The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).
Example:
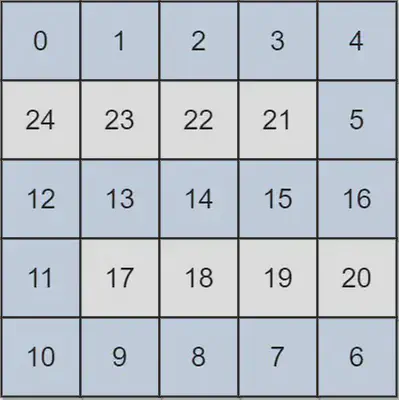
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation: The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
Key Ideas
- Use a min-heap to store the nodes and their corresponding time
- At any moment, we can only move to the node with elevation of at most the current time
- Traverse till the botton right node is reached and return the time
Code
import heapq
class Solution:
def swimInWater(self, grid: List[List[int]]) -> int:
# (t, (x,y))
# Maintain a min-heap to store the frontier nodes
# - Pop from the min-heap
# - choosing the node which has less wait time compared
n = len(grid)
DIRECTIONS = [(0,1), (1,0), (0,-1), (-1,0)]
queue = [(grid[0][0], (0,0))]
visited = set()
visited.add((0,0))
check_boundaries = lambda x, y: x >= 0 and x < n and y >= 0 and y < n
while queue:
t, (x,y) = heapq.heappop(queue)
if x == n-1 and y == n-1:
break
for dx,dy in DIRECTIONS:
xx = x+dx
yy = y+dy
if check_boundaries(xx,yy) and (xx,yy) not in visited:
heapq.heappush(queue, (max(t, grid[xx][yy]), (xx,yy)))
visited.add((xx,yy))
return t
Time complexity: O(nlogn),
Space complexity: O(n^2).
787. Cheapest Flights Within K Stops
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example:
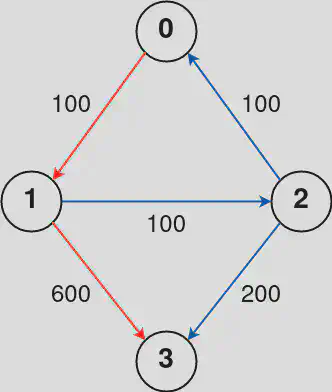
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Key Ideas
- Use a multisource BFS to search layer by layer
- Maintain a visited array to store the minimum cost to reach a node
- If the cost is greater than the cost in visited, then skip the node
- Else update visited and continue the search
code
from collections import deque, defaultdict
class Solution:
def findCheapestPrice(self,
n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
graph = defaultdict(dict)
for p, q, c in flights:
graph[p][q] = c
minCost = float("inf")
queue = deque([(0, src, K+1)])
visited = [float("inf")]*n
visited[src] = 0
while queue:
m = len(queue)
for _ in range(m):
cost, city, k = queue.popleft()
if k < 0 or cost > visited[city]:
continue
if city == dst:
minCost = min(minCost, cost)
visited[city] = cost
for adjcity, price in graph[city].items():
queue.append((price+cost, adjcity, k-1))
if minCost == float("inf"):
return -1
return minCost
127. Word Ladder
A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that:
- Every adjacent pair of words differs by a single letter.
- Every
sifor1 <= i <= kis inwordList. Note thatbeginWorddoes not need to be inwordList. sk == endWord
Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists.
Example:
Input: beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
Output: 5
Explanation: As one shortest transformation is “hit” -> “hot” -> “dot” -> “dog” -> “cog”, return its length 5.
Key Ideas
@IdeaThe entire problem can be thought of as a graph problem- The nodes are the words in the wordList
- The edges are the words which differ by a single letter
@IdeaUse a BFS to find the shortest path from beginWord to endWord- Create a pattern map;
pattern->List[word] - Perform multi-source BFS to keep track of the number of transformations
- The number of transformations is the layer at which
endWordis located frombeginWord
- The number of transformations is the layer at which
Code
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
"""
@Idea: BFS on the graph, when the endWord is reached return
the level at which it was located.
Algorithm:
1. Create the pattern mapping
2. Perform multi-source BFS from the beginWord
"""
if endWord not in wordList:
return 0
wordList.append(beginWord)
# pattern -> List of all words of the pattern
patternMap = collections.defaultdict(list)
n = len(beginWord)
for word in wordList:
for i in range(n):
pattern = word[:i]+"*"+word[i+1:]
patternMap[pattern].append(word)
transforms = 1
queue = collections.deque([beginWord])
visited = set([beginWord])
while queue:
m = len(queue)
for _ in range(m):
node = queue.popleft()
if node == endWord:
return transforms
for i in range(n):
pattern = node[:i]+"*"+node[i+1:]
for neigh in patternMap[pattern]:
if neigh not in visited:
queue.append(neigh)
visited.add(neigh)
transforms += 1
return 0